In ihrem Aufsatz „The Macroeconomics of Populism” haben die beiden Starökonomen Rüdiger Dornbusch und Sebastian Edwards Anfang der 1990er Jahre beschrieben, wie man in Lateinamerika mit Hilfe unseriöser Geld- und Fiskalpolitik wieder und wieder kurzfristige konjunkturelle Strohfeuer mit langfristig üblen Folgen entfachte. Mit übermäßiger Verschuldung heizte man die gesamtwirtschaftliche Nachfrage jenseits jeder makroökonomischen Vernunft an, was funktionierte, solange sich die Erwartungen der Wirtschaftsteilnehmer noch nicht auf die langfristig schädlichen Folgen solcher Politik eingestellt hatten. In der Zwischenzeit konnte man über seine Verhältnisse leben und kräftig Einkommen verteilen, die vermeintlich wie Manna vom Himmel fielen und für die auch langfristig scheinbar niemand bezahlen musste. Das war natürlich falsch, und am Ende kam die Rechnung immer. So taumelten diese Länder von einer Schuldenkrise in die nächste. Der tiefere Grund war stets der einfache Umstand, dass wir nicht im Schlaraffenland leben. Anders ausgedrückt: Wir Menschen können unseren Wohlstand immer nur unter der Beachtung einer Ressourcenbeschränkung mehren. Wir können nur konsumieren, was wir zuvor produziert hatten. Dass es heute makroökonomisch erneut so aussieht, als gäbe es keine Ressourcenrestriktion, ist eine andere und ziemlich komplexe Geschichte, die uns hier aber nicht weiter interessieren muss.
Wichtiger ist, dass man sich und anderen mit dem damaligen makroökonomischen Populismus vormachte, man könne die Grundregeln der Mathematik außer Kraft setzen. Es ist angesichts der Belastungen des Lockdowns nur allzu verständlich, dass sich diese Hoffnung auch im Umgang mit dem Coronavirus gerade wieder breitmacht. Vernünftig ist es trotzdem nicht. Grundlage dieser verständlichen Unvernunft ist die verlockend logisch klingende Annahme, man könne die Kontaktbeschränkungen etwas lockern, wenn man nur bereit wäre, dafür etwas höhere Inzidenzwerte in Kauf zu nehmen. In diesem Sinne äußerten sich viele Politiker, Verbandsvertreter und Journalisten, prominent unter ihnen beispielsweise Armin Laschet und Malu Dreyer. Man könne nicht immer allein auf Inzidenzwerte schauen, argumentierten sie, sondern man müsse auch andere Faktoren im Blick haben. Das klingt tatsächlich plausibel und sogar gerade von ökonomischem Vernunftdenken geleitet. Und doch verstößt es gegen zwingende mathematische Logik. Anders ausgedrückt: Es ist unmöglich, denn eine solche Abwägung gibt es nicht. Man möge diese Aussage nicht mit einer Wertung darüber verwechseln, ob man eine solche Abwägung vornehmen solle oder nicht. Diese Wertung wäre nachvollziehbar, wenn es sie gäbe. Aber es gibt sie nicht.
Warum nicht? Im Prinzip ist das ganz einfach. Kontaktbeschränkungen oder -lockerungen wirken zunächst einmal nicht auf die Inzidenz, sondern auf die Zahl derjenigen, die ein Infizierter seinerseits wieder infiziert. Das gibt der Reproduktionsfaktor oder R-Faktor wieder. Bei R=1 gibt jeder Infizierte im Durchschnitt einmal das Virus weiter. Erst jetzt kommt die Inzidenz ins Spiel: Bei R=1 bleibt sie im Zeitablauf nämlich gerade konstant. Das heißt: Wenn sie am Anfang 10 ist, dann bleibt sie konstant bei 10, solange R=1 ist. Ist sie am Anfang 60, dann bleibt sie bei 60, und ist sie am Anfang 500, dann bleibt sie bei 500. Wenn, ausgehend von R=1, die Kontaktbeschränkungen einmalig gelockert werden, dann steigt der R-Faktor einmalig auf einen Wert oberhalb von eins. Wer nun aber glaubt, dass auch die Inzidenz einmalig auf einen etwas höheren Wert steigt, der irrt sich. Vielmehr setzt der Anstieg von R auf einen Wert oberhalb von eins einen Prozess in Gang, innerhalb dessen die Inzidenz unaufhörlich und mit immer schnelleren Raten ansteigt, solange die Lockerung nicht zurückgenommen wird und R wieder gleich eins ist. Das ist der Grund, warum es kein Menü gibt, in dem man bestimmte Kontaktbeschränkungen zum Preis bestimmter Inzidenzwerte wählen kann.
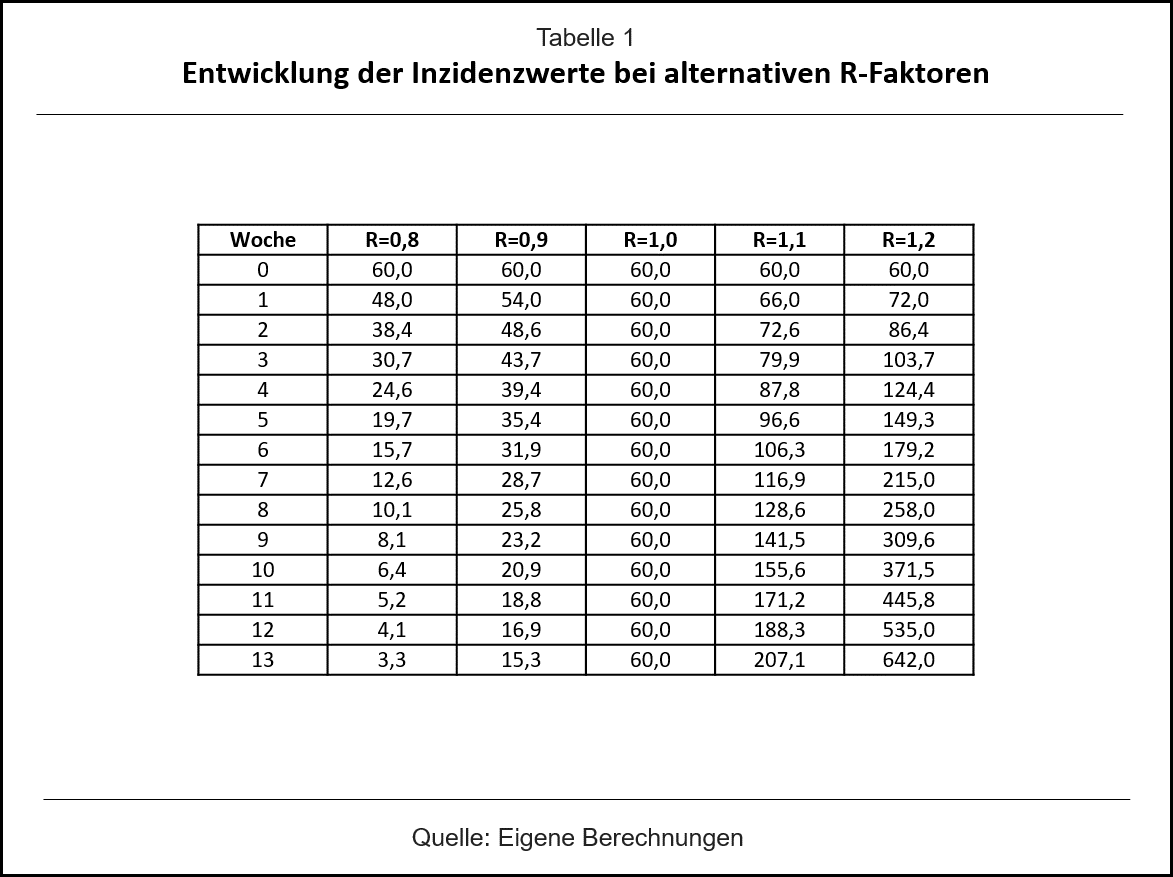
Die nachfolgende Tabelle verdeutlicht dies unter der Annahme, dass jeder Infizierte das Virus im Durchschnitt sieben Tage nach seiner eigenen Infektion weitergibt, was ungefähr der Realität entspricht. In der linken Spalte finden wir die Wochen, die vergehen, nachdem der R-Faktor einen gewissen Wert angenommen hat. In der oberen Zeile sind ein paar solcher R-Faktoren abgetragen, und zwar von 0,8 bis 1,2. Darunter findet sich jeweils die Entwicklung der Inzidenz, ausgehend von der Woche 0, mit einer angenommenen Inzidenz von 60. Auch das trifft ungefähr die derzeitige Realität.
– zum Vergrößern bitte auf die Grafik klicken –
Schauen wir erst einmal auf die dritte Spalte von rechts unterhalb von R=1, so sehen wir, dass die Inzidenz konstant bei 60 bleibt. Was geschieht, wenn wir von da aus Lockerungen zulassen, sehen wir in den beiden rechten Spalten bei R=1,1 und bei R=1,2. Für R=1,1 heißt das: Die Inzidenz steigt nicht einmalig, sondern sie steigt fortlaufend, nach 13 Wochen überschreitet sie die Grenze von 200. Von dort aus wird sie natürlich weiter steigen, und zwar immer schneller. Sollte der Reproduktionsfaktor auf R=1,2 steigen, was noch gar nicht so hoch ist, dann wird die Inzidenz bereits nach sieben Wochen über 200 liegen und nach 13 Wochen knapp 650 betragen. Das geht immer so weiter, solange die Politik die Lockerungen nicht zurücknimmt. Nimmt sie sie zurück, geht die Inzidenz aber nicht wieder auf ihren Ursprungswert von 60 zurück, sondern sie bleibt auf dem jeweils höheren Niveau. Beispiel: Wenn die Politik nach sieben Wochen Lockerungen mit R=1,2 wieder zu den ursprünglichen Kontaktbeschränkungen – also zum derzeitigen Lockdown – mit R=1 zurückkehrt, dann bleibt die Inzidenz anschließend bei 215.
Man beachte zwei Dinge. Erstens: Diese Zahlen beinhalten keinerlei Wertung. Zweitens: Die Zahlen sind nicht das Ergebnis eines irgendwie gearteten pessimistischen Szenarios. Sie sind völlig wertfrei und zeigen nicht mehr und nicht weniger als zwangsläufige Arithmetik. Damit zeigen sie aber auch dies: Sofern es gelingt, den R-Faktor konstant unter eins zu halten, dann sinkt die Inzidenz zwangsläufig und strebt gegen null. Das können wir an den beiden linken Spalten ablesen: Bei R=0,9 lägen wir nach 13 Wochen bei einer Inzidenz von gut 15, und bei R=0,8 bei 3,3.
Angesichts dieses so einfach nachvollziehbaren und öffentlich immer wieder erläuterten Zusammenhangs ist es erstaunlich, mit welcher Inbrunst wieder und wieder das Unmögliche diskutiert wird, nämlich die Abwägung zwischen Kontaktbeschränkungen und Inzidenz. Die Argumentation ist immer gleich, und sie findet immer auf der Werteebene statt: Wer für mehr Kontaktbeschränkungen ist, wertet offenbar die Gesundheit höher als die Freiheit, und wer für weniger Kontaktbeschränkungen ist, wertet offenbar die Freiheit höher als die Gesundheit. Aber jenseits einer Extremposition, gemäß derer man sogar die katastrophalen Folgen einer vollständigen Durchseuchung der Bevölkerung hinzunehmen bereit ist, sind solche Diskussionen gegenstandslos, weil sie auf der Annahme beruhen, man könnte die Gesetze der Arithmetik außer Kraft setzen.
Dies zeigt die nachfolgende Grafik. Auf der horizontalen Achse finden wir wiederum die Zeit und auf der vertikalen Achse die Inzidenz. Wieder starten wir mit einem Inzidenzwert von 60. Was geschieht, wenn der Reproduktionsfaktor konstant bei R=1 bleibt, zeigt die blaue Linie: er bleibt bei seinem Ausgangswert 60. Was bei R<1 geschieht, zeigt die rote Linie: Die Inzidenz sinkt mit der Zeit und nähert sich immer weiter der Null an.
– zum Vergrößern bitte auf die Grafik klicken –
Den populistischen Weg sehen wir anhand der schwarzen Linie. Am Ausgangspunkt mit einer angenommenen Inzidenz von 60 kann man im Prinzip den blauen, den roten oder den schwarzen Weg gehen. Nehmen wir an, es geschieht, was sich gerade in Deutschland abzeichnet: Die Kontaktbeschränkungen werden gelockert, ohne den treibenden Effekt der Lockerung auf R mit kompensatorischen Maßnahmen auszugleichen. Die Folge ist: R steigt zwangsläufig über eins, und ebenso zwangsläufig steigt die Inzidenz fortlaufend und immer schneller an, ohne dass dazu der R-Faktor weiter steigen müsste. Wir befinden uns auf dem aufsteigenden Ast der schwarzen Linie.
Das muss außer Kontrolle geraten. Irgendwann werden die Verhältnisse unerträglich, die Beispiele dafür kennen wir. Wenn man keine vollständige Durchseuchung mit all ihren Folgen hinnehmen will, dann wird man früher oder später beschließen müssen, die Lockerung wieder zurückzunehmen. Mehr noch: Weil eine Rückkehr zu R=1 lediglich die hohe Inzidenz stabilisiert und nicht wieder auf kleinere Werte zurückführt, müssen die Kontaktbeschränkungen so hart sein, dass der Reproduktionsfaktor auf R<1 und damit unter sein Ausgangsniveau sinkt. Denn nur dann sinkt die Inzidenz wieder ab, im Beispiel der schwarzen Linie am Ende wieder zurück auf 60.
Im Ergebnis hat die Politik schließlich entlang der schwarzen Linie einen vollständigen Infektionszyklus erzeugt, bei dem die Kontaktbeschränkungen im Durchschnitt wie im Falle der blauen Linie bei R=1 lagen. Weil man nämlich zeitweise bei R>1 und zeitweise bei R<1 lag, konnte man mit Blick auf die Strenge der Kontaktbeschränkungen nichts gewinnen, jedenfalls nicht im Durchschnitt. Daraus folgt: Jeder Versuch, die mathematische Logik des Infektionsgeschehens zu überlisten, führt entweder in die vollständige Durchseuchung der Bevölkerung oder in einen Infektionszyklus. Eine andere Option lassen die Grundregeln der Arithmetik nicht zu. Deshalb gibt es keine andere.
Das populistische am Verlauf der schwarzen Linie ist, dass man mit dem weniger strengen R>1 anfängt. Man fängt gewissermaßen damit an, über seine Verhältnisse zu leben, und verschiebt die Folgen auf später. Am Ende ist man wieder bei demselben Inzidenzwert, mit dem man begonnen hatte. Im Durchschnitt hat man mit R=1 dieselbe Inzidenz gehabt, wie bei der blauen Linie. So gesehen scheint es, als hätte man nichts gewonnen und nichts verloren. Aber das ist nur die halbe Wahrheit. Hier ist die andere Hälfte: Zu den ursprünglich 60 infizierten Personen pro sieben Tage und pro 100 Tsd. Einwohnern hat es zusätzliche Infektionen gegeben. Die Summe der zusätzlich Infizierten entspricht der Fläche unterhalb der schwarzen Kurve und oberhalb der blauen Linie. Sie repräsentiert die zusätzliche Belastung unseres Gesundheitssystems, zusätzliche Quarantäne, zusätzliche Krankschreibungen, zusätzliche Long-Covid-Erkrankte und zusätzliche Sterbefälle. Je länger man sich R>1 geleistet hat, desto größer diese Fläche und desto schlimmer sind die Folgen.
Der Öffnungspopulismus ist also nicht nur sinnlos, er kommt uns vielmehr teuer zu stehen. Er hat eigentlich nur Kosten: wirtschaftliche Kosten, gesellschaftliche Kosten und gesundheitliche Kosten. Er bietet uns auf der Habenseite keine zusätzlichen Freiheiten und keine wirtschaftlichen oder gesellschaftlichen Erleichterungen, weil wir uns alles das nur in einer kurzen Periode vormachen, um es anschließend mit umso härteren Einschränkungen unserer Freiheiten sowie mit umso härteren wirtschaftlichen und gesellschaftlichen Einschränkungen bezahlen müssen. Populistische Infektionszyklen folgen einer ganz ähnlichen Logik wie makroökonomischer Populismus, mit allerdings einem Unterschied: Während die Analyse des makroökonomischen Populismus auf dem sehr umstrittenen Konzept der Phillips-Kurve beruht, steht die Arithmetik des Öffnungspopulismus auf sehr sicheren Füßen und kann überhaupt nicht ernsthaft bestritten werden. Tatsächlich wird sie in der Fachwelt auch von Niemandem in Zweifel gezogen, auch wenn man die Dinge dort nicht in einen politischen Entscheidungszusammenhang einbindet.
In einem Interview bei Sandra Maischberger sagte der österreichische Bundeskanzler Sebastian Kurz: „Bekanntlich verläuft die Covid-Pandemie in Zyklen.“ Im Prinzip hat er damit recht, weil sich die bisherige Entwicklung damit zutreffend beschreiben lässt. Was er aber nicht gesagt hat und was ihm vermutlich auch nicht klar gewesen ist, das ist die Ursache der Zyklen: Die hat nämlich nichts mit den naturwissenschaftlichen Eigenarten der Pandemie zu tun, sondern mit der Art und Weise, wie die Politik mit der Pandemie umgeht. Geht sie populistisch damit um, dann verläuft sie zyklisch. Das Schlimme ist: Wir stehen in Deutschland gerade zum zweiten Mal am Anfang eines öffnungspopulistischen Infektionszyklus. Bei hohen und steigenden Infektionswerten und trotz eines R-Faktors von etwa 1,1 werden allenthalten Öffnungen verkündet, und fast immer mit dem Argument, dass man nicht allein auf Inzidenzwerte blicken dürfe. Es steht zu befürchten, dass der Schaden dieser zweiten populistisch verursachten Welle groß sein wird; vielleicht wird es der größte, den wir bisher hatten. Hoffen wir, dass es nicht so kommt. Besser wäre freilich, wir würden mehr tun als zu hoffen.
Zur Ehrenrettung der verantwortlichen Politiker muss gewiss festgehalten werden, dass man nicht bewusst falsch handeln muss, um Öffnungspopulismus zu betreiben. Es reicht, wenn man sich selbst etwas vormacht. Daher gibt es keinen Grund, an der Ehrenwertigkeit ihrer Absichten zu zweifeln. Das ist bei jenen vieldiskutierten Populisten anders, die derzeit unsere Demokratien böswillig angreifen. Umso dringender ist den Öffnungspopulisten anzuraten, sich die Zeit dazu zu nehmen, sich die Zwangsläufigkeit der Infektionsdynamik noch einmal konsequent vor Augen zu führen. Denn darin liegt der Schlüssel zu einer nachhaltigen Strategie, die von vielen gefordert wird, allerdings meist, ohne auch nur einen Hinweis darauf zu geben, wie eine solche nachhaltige Strategie aussehen könnte. Hier ein paar Elemente:
- Was immer die Politik unternimmt, es muss immer im Rahmen eines R-Faktors sein, der gleich oder kleiner ist als eins. Es ist richtig, wenn Politiker und Beobachter fordern, dass man mit Phantasie und Tatkraft unterschiedliche Instrumente entwickeln, einsetzen und ausprobieren sollte. Falsch ist, dass der R-Faktor zu diesen Instrumenten gehören darf. Stattdessen sollte die Regel lauten: Du darfst alles, nur nicht den R-Faktor über eins wachsen lassen. Nennen wir sie die R<1-Regel. Sie ist ganz analog zu der Regel, dass man auf Dauer nicht über seine Verhältnisse leben darf. Wenn wir grobe Kontaktverbote aufheben und zugleich eine geeignete Teststrategie einsetzen, so dass wir in der Kombination der Maßnahmen die R<1-Regel beachten, dann ist das ein Erfolg. Aber wenn wir ein Maßnahmenpaket durchsetzen, das die Regel verletzt, dann ist das ein Misserfolg, denn dann leben wir über unsere Verhältnisse und werden später dafür bezahlen müssen.
- Weil jede Lockerung der Kontaktbeschränkungen den R-Faktor erhöht, muss sie also durch Maßnahmen kompensiert werden, die den R-Faktor senken. Wir müssen uns bei Beachtung der R<1-Regel die Aufhebung der Kontaktbeschränkungen Schritt für Schritt erarbeiten, durch Nachverfolgung, durch Testen, durch Impfen und wer weiß, durch welche innovativen anderen Methoden noch. Alles das senkt den R-Faktor. Aber immer gilt: Zuerst muss die Voraussetzung für eine Lockerung geschaffen werden, und erst dann kann die Lockerung selbst erfolgen. Sonst wird die R<1-Regel verletzt. Für die Schulen haben uns das die Österreicher vorgemacht: Zuerst wurde eine geeignete Teststrategie entwickelt (kurz: Wer das Schulgebäude betritt, muss vorher negativ getestet worden sein); dann wurden die Schulen geöffnet. Man vergleiche die deutsche Strategie damit: Erst wurden die Schulen (teilweise) geöffnet, dann begann man eine Diskussion, ob eine Teststrategie für Schulen vielleicht sinnvoll sein könnte. Das verletzt die R<1-Regel, und es wird sich rächen.
- Die Politik muss Anreize zur dezentralen und möglichst individuellen Entwicklung solcher Verhaltensweisen setzen, die den R-Faktor senken. Auch hierzu sind die Beispiele längst bekannt: Wer in Israel ins Kino will, muss entweder genesen, geimpft oder getestet sein. Das treibt die Leute dazu, sich impfen zu lassen und damit ganz nebenbei zur Herdenimmunität beizutragen. Wer das nicht will oder kann, erschließt sich Freiheit durch Testen. In jedem Falle arbeitet jeder aus eigenem Interesse daran, dass man sich gemeinsam die alten Freiheiten zurückholt – nicht vom Staat, sondern von dem Virus!
Alle diese Instrumente gibt es schon, oder sie sind in greifbarer Nähe. Wir müssen nur endlich beherzt zugreifen. Wir tun es aber nicht zuletzt deshalb nicht, weil wir dem Öffnungspopulismus auf den Leim gehen. Seine Tücke ist: Mit ihm kaufen wir uns Zeit und verschwenden sie sogleich für Dinge, die uns von der Entwicklung wirklich tragfähiger Perspektiven abhalten. So tun wir das jetzt seit einem dreiviertel Jahr! Überwinden wir den Öffnungspopulismus also, und folgen wir der R<1-Regel. Sie treibt uns dazu an, Voraussetzungen zu schaffen, die es uns anschließend erlauben, die Kontaktbeschränkungen zu lockern. Nur damit erschließen wir uns die so oft und zurecht geforderte Perspektive.
- Populismus und Verschwörungstheorien - 13. April 2024
- Reform der Schuldenbremse!? - 7. Dezember 2023
- Der Universalismus und die Zukunft des Westens - 26. August 2023



Eine „Maßnahme“ von Mutter Natur ist nicht berücksichtigt – nämlich der saisonale Effekt, den wir letztes Jahr beobachten konnten. In dreizehn Wochen beginnt schon der Juni.
Wenn man es mit den Lockerungen nicht übertreibt, kann es trotzdem gelingen, dass der geometrische Mittelwert von R unter eins bleibt.
Fehlendes ökonomisches Wissen oder politisches Kalkül?
Professor Thomas Apolte ruft in dem obigen sehr lesenswerten Artikel zur Ehrenrettung der in der Coronakrise Verantwortung tragenden Politiker auf. Dies vor allem, weil oft nicht bewusst falsch gehandelt worden sei, um Öffnungspopulismus zu betreiben. Diese Sichtweise ist in Bezug auf die meisten unter Unsicherheit verantwortlich handelnden Politiker auch aus meiner Perspektive völlig zutreffend.
Dennoch stellt sich die Frage, ob hiervon nicht vielleicht Teile der Politiker auszunehmen wären, wenn man sich gewisse Zusammenhänge noch einmal vor Augen führt. Dies ist offensichtlich für die Politikerinnen und Politiker, die noch immer vor die Gefahren der Pandemie offensichtlich herunterspielen und praktisch vollständig für individuelle Eigenverantwortung zu ihrer Bekämpfung eintreten, obwohl dies offensichtlich und auch empirisch nachweisbar auch aus einer ökonomischen Perspektive und bei Beachtung verschiedener wichtiger und zu beachtender Zielkonflikte nicht ausreicht.
Spannender ist aber wohl die Frage, ob das Argument von Professor Apolte rund 10 Monate nach Veröffentlichung seines Beitrags auch für die Politiker einer Partei gilt, deren Parteiangehörige auf eine lange freiheitliche Tradition zurückblicken können und auch wichtige Weichenstellungen Deutschlands mitverantworte und die alles in allem eindeutig als im besten Sinne demokratisch zu gelten hat. Diese Partei hat bis zur Bundestagswahl 2021 nicht nur selbst gemäß dem verankerten eigenen Bewusstsein regelmäßig bei der Coronavirus-Bekämpfung gemäß der Verfassung gehandelt. Darüber hinaus haben deren zentrale Repräsentanten seit 2020 den Vertretern der bisherigen Bundesregierung vielfach und medial stark wahrgenommen vorgeworfen, bei vielen getroffenen Maßnahmen während der Corona-Pandemie Verfassungsgrundsätze missachtet zu haben.
Hierbei sticht als Speerspitze der Kritik insbesondere der Bundestagsabgeordnete der FDP und Jurist W. Kubicki heraus, der sogar ein äußerst kritischen Buch zum Thema verfasst hat. Auffällig ist, dass er in seiner Argumentation systematisch die wesentliche Problematik von „technologischen externen Effekten“ ausblendet, obwohl er auch studierter Volkswirtschaft ist und eine Wissensauffrischung zu diesem Gebiet sehr leicht allgemein ( https://www.staatslexikon-online.de/Lexikon/Externe_Effekte) und auch mit Bezug direkt zur derzeitigen Pandemie (https://bcf.princeton.edu/the-resilient-society/ oder auch hier: https://www.econstor.eu/handle/10419/231886) möglich wäre und sicherlich auch angezeigt ist, wenn man sich sehr häufig prominent zu dieser Thematik in den Medien äußert.
Ob von Verfechtern der Eigenverantwortungsthese auch in Pandemien generell und von W. Kubicki im Besonderen die Externalitäts-Problematik in einem gesamtgesellschaftlichen Zusammenhang erkannt bzw. in ihrer Tragweite durchdrungen worden ist, ist zumindest unklar, weil es etwa in einem gerade erschienenen Artikel des stellvertretenden FDP-Vorsitzenden heißt: „Wenn eine Impfung nachweislich nicht vor der Infektion anderer schützt, warum ist eine solche dann ein Ausweis der gesellschaftlichen Solidarität?“ (https://www.welt.de/debatte/kommentare/plus235692852/Kubicki-zu-Corona-Kritische-Phase-des-freiheitlichen-Rechtsstaats.html).
Auch andere führende und vor allem juristisch ausgebildete Politiker der ja in der Regel als Freiheits- und Wirtschaftspartei bekannten FDP argumentieren in vielerlei Hinsicht damit, dass in der Pandemie in erster Linie die Eigenverantwortung zählen solle und die Verhältnismäßigkeit bei den Maßnahmen der Politik gegen die Coronapandemie allzu oft zumindest bis zur Bundestagswahl nicht gewahrt worden sei. W. Kubicki wagte sogar in seinem Beitrag die Aussage, dass „die Einschätzung mancher Beobachter nachvollziehbar“ sei, „Karlsruhe habe nach mehr als anderthalb Jahren Pandemie nicht zum Rechtsfrieden beigetragen.“
Genau vor diesem Hintergrund stellt sich die Frage, ob mangelnde Informiertheit oder politisches Kalkül der Grund für die politische Positionierung von einigen führenden Politikern der FDP in der Corona-Debatte bis zur Bundestagswahl und´zumindest in Teilen der Partei auch jetzt noch ist.
So heißt es aktuell im Handelsblatt: „Noch im Wahlkampf hatte die Oppositon gegen die von der Großen Koalition verhängten Coronaregeln der FDP zu vielen Unterstützern verholfen. Eine demokratische Partei, die konstruktive Kritik an den Einschränkungen des Infektionsschutzgesetzes äußert, kam bei Wählerinnen und Wählern gut an“ (https://www.handelsblatt.com/politik/deutschland/pandemie-die-impfpflicht-und-die-freiheit-coronapolitik-sorgt-fuer-aerger-in-der-fdp-/27914222.html?ticket=ST-6038985-sc4XeetRpvKMKIMLXPFz-cas01.example.org).
Es stellt sich aber angesichts des versteckten Werturteils in diesem Sachartikel die Frage, ob wirklich von „konstruktiver Kritik“ die Rede sein kann, wenn charakteristische ökonomische Aspekte des pandemischen Grundproblems in Bezug auf negative und positive „technologische“ externe Effekt einfach in der Argumentation führender Politiker eine Wirtschaftspartei offensichtlich ausgeblendet bleiben. Dies ist recht schwer nachvollziehbar vor dem Hintergrund, dass das Thema sehr früh von führenden US-Ökonomen publikumswirksam aufgegriffen worden ist (https://eu.usatoday.com/story/opinion/2020/04/30/coronavirus-tests-quarantines-incentives-can-make-it-work-column/3048508001/) und obwohl ebenfalls etwa Professor Apolte mehrfach auf die zentralen ökonomischen Sachverhalte und Dilemmata in einer Pandemie hingewiesen hat (etwa hier: http://wirtschaftlichefreiheit.de/wordpress/?p=28519).
Den Leserinnen und Lesern dieses Kommentars bleibt es überlassen, die zu Beginn gestellte Frage selbst zu beantworten.
Abschließend ist festzustellen: Es ist spannend zu sehen, wie die verschiedenen Politiker sich am Ende individuell im Bundestag zur Impfflicht positionieren werden. Nicht auszuschließen ist ja, dass alle ausgesprochenen Gegner einer allgemeinen Impfflicht selbst in höchster Not in einer Pandemie mit sehr hohen Kollateralschäden für Gesellschaft und Wirtschaft sich der Position einer Gruppe von FDP-Politikern anschließen, die die allgemeine Impfflicht bei Corona trotz des rapide geänderten Virus trotzdem ablehnen wollen. Dies bedeutet allerdings auf der anderen Seite, dass die Freiheit insbesondere auch diejenigen, die der Eigen- und zugleich der gebührenden Fremdverantwortung durch Vorsichtsmaßnahmen und eigene Impfung zur Wahrung auch der Freiheit von anderen wirklich soweit wie möglich gerecht geworden sind, de facto eingeschränkt wird. Anders ausgedrückt: Würde es zu einer gemeinsamen Abstimmung aller Gegner einer allgemeinen Impfflicht im Bundestag zusammen mit den bisher über 20 sich dazu bekennenden FDP-Politikern kommen, könnten sich die Fronten in dieser Sache wohl für viele noch transparenter als bisher darstellen.